已知直线 的参数方程为
的参数方程为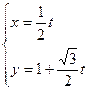 (
(
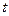 为参数),曲线
为参数),曲线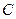 的极坐标方程为
的极坐标方程为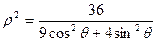
(1) 写出直线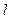 的极坐标方程与曲线
的极坐标方程与曲线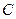 的普通方程;
的普通方程;
2)以极点为原点 ,极轴为
,极轴为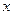 轴正方向建立
轴正方向建立 直角坐标系,设直线
直角坐标系,设直线 与曲线
与曲线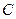 交于
交于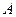 ,
,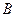 两点,求
两点,求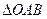 的面积.
的面积.
设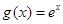 ,
, ,其中
,其中 是常数,且
是常数,且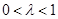 .
.
(1)求函数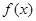 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数 ,使不等式
,使不等式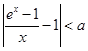 成立;
成立;
(3)设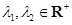 ,且
,且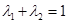 ,证明:对任意正数
,证明:对任意正数 都有:
都有: .
.
已知二次函数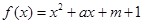 ,关于x的不等式
,关于x的不等式 的解集为
的解集为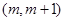 ,其中m为非零常数.设
,其中m为非零常数.设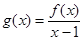 .
.
(1)求a的值;
(2)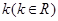 如何取值时,函数
如何取值时,函数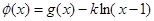 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若m=1,且x>0,求证: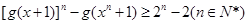
设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),求证:{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn+1(n=1,2,3,…).
设命题p:关于x的不等式2|x-2|<a的解集为;命题q:函数y=lg(ax2-x+a)的值域是R.如果命题p和q有且仅有一个正确,求实数a的取值范围.
已知命题p:函数y=loga(1-2x)在定义域上单调递增;命题q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若p∨q是真命题,求实数a的取值范围.