设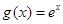 ,
, ,其中
,其中 是常数,且
是常数,且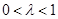 .
.
(1)求函数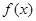 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数 ,使不等式
,使不等式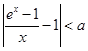 成立;
成立;
(3)设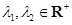 ,且
,且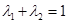 ,证明:对任意正数
,证明:对任意正数 都有:
都有: .
.
“坐标法”是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究图形的几何性质的方法,它是解析几何中是基本的研究方法. 请用坐标法证明下面问题:
已知圆O的方程是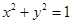 ,点
,点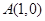 ,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是
,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是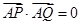 .
.
已知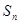 是等比数列{
是等比数列{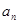 }的前
}的前 项和,
项和, 、
、 、
、 成等差数列.
成等差数列.
(Ⅰ)求数列{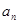 }的公比
}的公比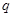 ;
;
(Ⅱ)求证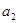 、
、 、
、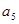 成等差数列.
成等差数列.
已知椭圆C的两焦点分别为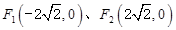 ,长轴长为6.
,长轴长为6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.
在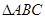 中,内角
中,内角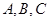 对边分别为
对边分别为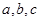 ,且
,且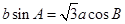 .
.
(Ⅰ)求角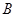 的大小;
的大小;
(Ⅱ)若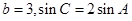 ,求
,求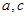 的值.
的值.
已知椭圆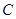 的中心为坐标原点O,焦点在
的中心为坐标原点O,焦点在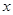 轴上,离心离为
轴上,离心离为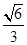 ,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为
,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为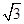 .
.
(Ⅰ)求椭圆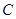 的方程;
的方程;
(Ⅱ)设过点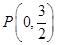 的直线
的直线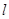 与椭圆
与椭圆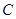 交于
交于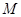 ,
,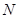 两点,且
两点,且 ,求直线
,求直线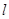 的方程.
的方程.