数列 的前
的前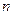 项和为
项和为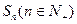 ,点
,点 在直线
在直线 .
.
⑴求数列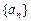 的通项公式;
的通项公式;
⑵ 数列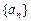 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
的内角 的对边分别为 ,已知 , ,求 .
对于数对序列
,记
,
,其中
表示
和
两个数中最大的数.
(1)对于数对序列
,求
的值;
(2)记 为 四个数中最小的数,对于由两个数对 组成的数对序列 和 ,试分别对 和 两种情况比较 和 的大小;(3)在由五个数对 组成的所有数对序列中,写出一个数对序列 使 最小,并写出 的值.(只需写出结论).
已知椭圆
.
(1)求椭圆
的离心率;
(2)设
为原点,若点
在椭圆
上,点
在直线
上,且
,试判断直线
与圆
的位置关系,并证明你的结论.
已知函数
.
(1)求证:
;
(2)若
对
恒成立,求
的最大值与
的最小值.
如图,正方体 的边长为2, 分别为 的中点,在五棱锥 中, 为棱 的中点,平面 与棱 , 分别交于 , .
(1)求证:
;
(2)若
底面
,且
,求直线
与平面
所成角的大小,并求线段
的长.