已知数列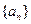 的前
的前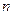 项和
项和 。(1)求数列的通项公式
。(1)求数列的通项公式
;(2)求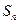 的最大或最小值。
的最大或最小值。
已知圆 与两坐标轴都相切,圆心
与两坐标轴都相切,圆心 到直线
到直线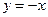 的距离等于
的距离等于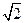 .
.
(1)求圆 的方程;
的方程;
(2)若圆心在第一象限,点 是圆
是圆 上的一个动点,求
上的一个动点,求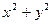 的取值范围.
的取值范围.
对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[ ]
]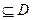 ,使
,使 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把 (
(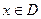 )叫闭函数。
)叫闭函数。
(1)求闭函数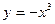 符合条件②的区间[
符合条件②的区间[ ];
];
(2) 判断函数
判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若函数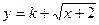 是闭函数,求实数
是闭函数,求实数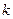 的取值范围
的取值范围
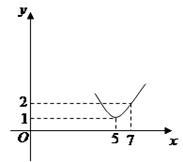
据预测,我国在“十二五”期间内某产品关税与市场供应量 的关系近似地满足
的关系近似地满足 :
: (其中
(其中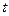 为关税的税率,且
为关税的税率,且 ,
, 为市场价格,
为市场价格,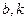 为正常数),当
为正常数),当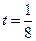 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;
(1)根据图象求 的值;
的值;
(2)若市场需求量为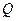 ,它近似满足
,它近似满足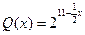 .
.
当 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率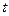 的最小值.
的最小值.
已知定义域为 的函数
的函数 是奇函数。
是奇函数。
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的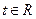 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
已知函数 ,且f(1)=
,且f(1)=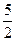 ,f(2)=
,f(2)= .(1)求
.(1)求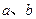 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在 上的单调性,并证明。
上的单调性,并证明。