(本小题满分13分)(第一问8分,第二问5分)
已知函数f(x)=2lnx,g(x)= ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[f′(x)-g′(x)]=-3x2-(a+6)x+1.其中f′(x),g′(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由.
(本小题满分14分)如图,四边形 为矩形,
为矩形,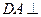 平面
平面 ,
,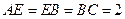 ,
,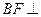 平面
平面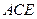 于点
于点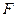 ,且点
,且点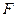 在
在 上,点
上,点 是线段
是线段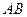 的中点。
的中点。
(1)求证: ;
;
(2)求三棱锥 的体积;
的体积;
(3) 试在线段
试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 。
。
(本小题满分12分)已知圆 和
和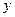 轴相切,圆心在直线
轴相切,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为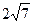
 ,求圆
,求圆 的方程
的方程
、(本小题满分12分)某市统计局就某地居民的月收入调查了10000人,他们的月收入均在 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在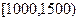 内)
内)
(1)求 某居民月收入在
某居民月收入在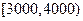 内的频率;
内的频率;
(2)根据该频率分布直方图估计居民的月收入的中位数; (3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在
(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在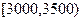 内的居民中抽取多少人?
内的居民中抽取多少人?
已知函数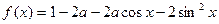 的最小值为
的最小值为 .
.
(1)求
(2)若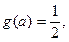 求
求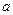 及此时
及此时 的最大值.(12分)
的最大值.(12分)
设函数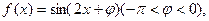
 图象的一条对称轴是直线
图象的一条对称轴是直线 .
.
(1)求 的值;
的值;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)在下图中画出函数 在区间
在区间 上的图像.(12分)
上的图像.(12分)