已知圆 过点
过点
 ,且与圆
,且与圆
 (
( >0)关于直线
>0)关于直线 对称,
对称,
⑴求圆 的方程;
的方程;
⑵过点 作两条直线分别与圆
作两条直线分别与圆 相交于点
相交于点 、
、 ,且直线
,且直线 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,判断直线
为坐标原点,判断直线 与
与 是否平行,并请说明理由
是否平行,并请说明理由
已知直线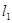 经过点A
经过点A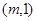 ,B
,B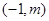 ,直线
,直线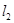 经过点P
经过点P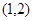 ,Q
,Q 。
。
⑴若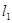 //
//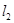 ,求
,求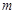 的值;
的值;
⑵若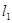 ⊥
⊥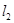 ,求
,求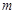 的值。
的值。
如图,在长方体ABCD—A1B1C1D1中,AA1=AD=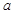 ,AB=2
,AB=2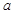 ,E,F分别为C1D1,
,E,F分别为C1D1,
A1D1的中点。
⑴求证:DE/⊥平面BCE;
⑵求证:AF//平面BDE。
已知函数
(Ⅰ)①判断函数的奇偶性,并加以证明;
②若 (-1,1),计算
(-1,1),计算 ;
;
(Ⅱ)若函数 在
在 上恒有零点,求实数m的取值范围;
上恒有零点,求实数m的取值范围;
(Ⅲ)若n为正整数,求证: .
.
已知函数
的部分图象如下图所示。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)若不等式 在
在 上
上
恒成立,求实数m的取值范围。
已知函数
(Ⅰ)当 时,求f(x)的最大值与最小值;
时,求f(x)的最大值与最小值;
(Ⅱ)若f(x)在 上是单调函数,且
上是单调函数,且 ,求θ的取值范围。
,求θ的取值范围。