如图所示,△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,若AC=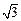 .求线段AD的长.
.求线段AD的长.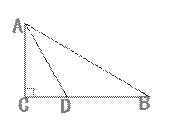
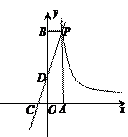
点P(1, )在反比例函数
)在反比例函数 的图象上,点P关于
的图象上,点P关于 轴的对称点在一次函数
轴的对称点在一次函数 的图象上,求此反比例函数的解析式
的图象上,求此反比例函数的解析式

以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是 的切线,连接OQ. 求
的切线,连接OQ. 求 的大小;
的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被 截得的弦长
截得的弦长
如图一,AB是 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和 相切与点C,
相切与点C, ,垂足为D.
,垂足为D.
(1)求证 ;
;
(2)如图二,若把直线EF向上移动,使得EF与 相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与
相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.