某商品的进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当售价的范围是是多少时,使得每件商品的利润率不超过80%且每个月的利润不低于2250元?
如图,AB为⊙O的直径,C为⊙O上的点,PA切于⊙O于点A,PA=PC,∠BAC=30°,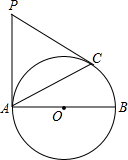
(1)求证:PC是⊙O的切线;
(2)若⊙O的半径为1,求PC的长(结果保留根号).
如图,在直角坐标系,点P的坐标为(-6,8)将OP绕点O顺时针旋转90°得到线段OP′.
(1)在图中画出OP′;
(2)点P′的坐标为;
(3)求线段PP′的长度.
在一个不透明的口袋中装有3个完全相同的小球,把它们分别标号为1,2,3,随机地摸出一个小球然后放回,再随机地摸出一个小球.
(1)两次摸出的小球的标号不同的概率为;
(2)求两次摸出小球的标号之积是3的倍数的概率(采用树形图或列表法).
解方程
(1)
(2)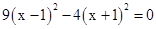
如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AB于E.
(1)证明△PAE∽△CDP;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设AP=x,BE=y,求y与x的函数关系式及y的取值范围;
(3)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由.