如图.AD、AH分别是△ABC(其中AB>AC)的角平分线、高线,M点是AD的中点,△MDH的外接圆交CM于E,求证∠AEB=90°。
(本题10分)如图,已知△ABC中,∠A=90°,AC=10,AB=5,点A、C分别在x轴和y轴上,且C(0,8),抛物线y=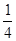 x2+bx+c过B、C两点
x2+bx+c过B、C两点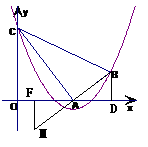
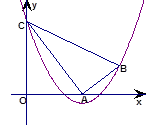
⑴求抛物线解析式.
⑵如果将△ABC沿CA翻折,设点B的落点为点M,现平移抛物线,使它的顶点为M,求出平移后的抛物线解析式,并写出平移的方法.
(本题10分)如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD
于E交AD 的延长线于F,DC=2AD,AB=BE
的延长线于F,DC=2AD,AB=BE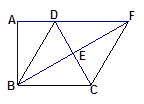
⑴求证:AD=DE.
⑵判断四边形BCFD的形状并说明理由.
(本题10分)为了解八年级学生的课外阅读情况,我校语文组从八年级随机抽取了若干名学生,对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图,请你依据图中提供的信息,解答下列问题:(每组含最小值不含最大值)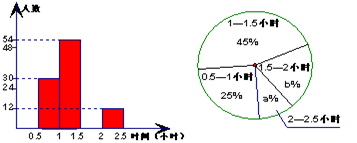
⑴从八年级抽取了多少名学生?
⑵填空 (直接把答案填到横线上)
①“2—2.5小时”的部分对应的扇形圆心角为_______度;
②课外阅读时间的中位数落在________(填时间段)内.⑶如果八年级共有800名学生,请估算八年级学生课外阅读时间
不少于1.5小时的有多少人?
(本题8分)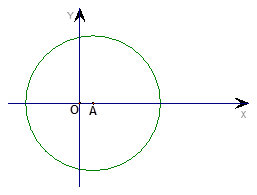 如图,在一次课外数学实践
如图,在一次课外数学实践 活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据:
活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据:
 ≈1.41,
≈1.41,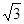 ≈1.73)
≈1.73)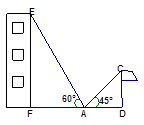
(本题8分)双休日,甲、乙、丙三人去A、B两超市购物,如果三人去A、B两超市的机会均等.(1)用画树状图的方法(或枚举法)表示出三人去超市的所有等可能结果;
(2)求出一人去A超市两人去B超市的概率.