(本小题满分12分)某加工厂需要定期购买原材料,已知每公斤材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(1)设该厂每 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在 天内总的保管费用
天内总的保管费用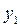 关于
关于 的函数关系式;
的函数关系式;
(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用 最少,并求出这个最少(小)值.
最少,并求出这个最少(小)值.
1.已知数列 ,其中
,其中 ,且数列
,且数列 为等比数列,求常数
为等比数列,求常数 .
.
2.设
 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明数列
,证明数列 不是等比数列.
不是等比数列.
设Sn为等差数列{an}的前n项和.(n∈N*).
(Ⅰ)若数列{an}单调递增,且a2是a1、a5的等比中项,证明:
(Ⅱ)设{an}的首项为a1,公差为d,且 ,问是否存在正常数c,使
,问是否存在正常数c,使 对任意自然数n都成立,若存在,求出c(用d表示);若不存在,说明理由.
对任意自然数n都成立,若存在,求出c(用d表示);若不存在,说明理由.
已知等比数列 及等差数列
及等差数列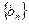 ,其中
,其中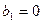 ,公差
,公差 ,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和
,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和
设等差数列 的前n项和为
的前n项和为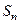 ;设
;设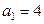 ,问
,问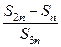 是否可能为一与n无关的常数?若不存在,说明理由.若存在,求出所有这样的数列的通项公式.
是否可能为一与n无关的常数?若不存在,说明理由.若存在,求出所有这样的数列的通项公式.
已知数列 成等差数列,
成等差数列,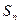 表示它的前
表示它的前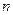 项和,且
项和,且 ,
, .
.
⑴求数列 的通项公式
的通项公式 ;
;
⑵数列 中,从第几项开始(含此项)以后各项均为负数?
中,从第几项开始(含此项)以后各项均为负数?