已知奇函数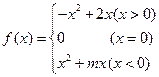
(1)求实数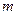 的值,并在给出的直角坐标系中画出
的值,并在给出的直角坐标系中画出 的图象;
的图象;
(2)若函数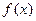 在区间
在区间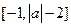 上单调递增,试确定实数
上单调递增,试确定实数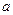 的取值范围.
的取值范围.
在上海世博会期间,小红计划对事先选定的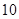 个场馆进行参观.在她选定的
个场馆进行参观.在她选定的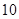 个场馆中,有
个场馆中,有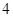 个场馆分布在
个场馆分布在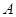 区,
区,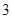 个场馆分布在
个场馆分布在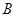 区,
区,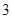 个场馆分布在
个场馆分布在 区.已知
区.已知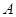 区的每个场馆的排队时间为
区的每个场馆的排队时间为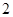 小时,
小时,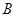 区和
区和 区的每个场馆的排队时间为
区的每个场馆的排队时间为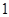 小时.参观前小红因事只能从这
小时.参观前小红因事只能从这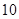 个场馆中随机选定
个场馆中随机选定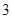 个场馆进行参观.
个场馆进行参观.
(Ⅰ)求小红每个区都参观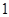 个场馆的概率;
个场馆的概率;
(Ⅱ)设小红排队时间总和为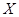 (小时),求随机变量
(小时),求随机变量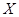 的分布列和数学期望
的分布列和数学期望 .
.
设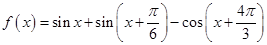 .
.
(Ⅰ)求函数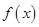 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(Ⅱ)若锐角 中,
中, 的对边分别为
的对边分别为 且
且 ,
, ,
, ,求角
,求角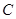 及边
及边 .
.
(本小题满分14分)已知函数
(Ⅰ)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的最小值;
的最小值;
(Ⅱ)方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围;
(Ⅲ)在函数 的图象上是否存在不同两点
的图象上是否存在不同两点 ,线段
,线段 的中点的横坐标为
的中点的横坐标为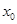 ,有
,有 成立?若存在,请求出
成立?若存在,请求出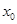 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分14分)已知直线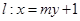 过椭圆
过椭圆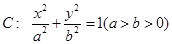 的右焦点
的右焦点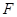 ,抛物线
,抛物线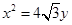 的焦点为椭圆
的焦点为椭圆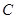 的上顶点,且直线
的上顶点,且直线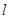 交椭圆
交椭圆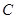 于
于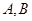 两点.
两点.
(1)求椭圆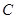 的方程;
的方程;
(2)若直线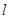 交
交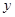 轴于点
轴于点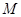 ,且
,且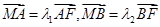 ,当
,当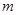 变化时,
变化时, 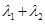 的值是否为定值?若是,求出这个定值,若不是,说明由.
的值是否为定值?若是,求出这个定值,若不是,说明由.
(本小题满分13分) 已知数列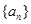 的前
的前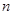 项和是
项和是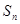 ,且
,且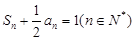 .
.
(1)求数列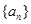 的通项公式;
的通项公式;
(2)设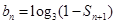 ,求适合方程
,求适合方程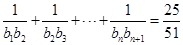 的正整数
的正整数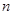 的值.
的值.