已知函数 (
(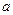 ,
, 均为正常数) .
均为正常数) .
(1)若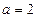 ,求函数
,求函数 在区间
在区间 上的单调减区间;
上的单调减区间;
(2)设函数在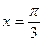 处有极值.
处有极值.
①对于一切 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
②若函数f (x)在区间 上是单调增函数,求实数
上是单调增函数,求实数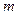 的取值范围.
的取值范围.
(本小题满分12分)
在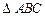 中,角
中,角 ,
,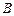 ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,向量
,向量 ,
, ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
(本小题满分13分)
在平面直角坐标系中,已知点 ,点
,点 在直线
在直线 上运动,过点
上运动,过点 与
与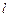 垂直的直线和
垂直的直线和 的中垂线相交于点
的中垂线相交于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设点 是轨迹
是轨迹 上的动点,点
上的动点,点 ,
, 在
在 轴上,圆
轴上,圆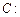
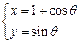 (
( 为参数)内切于
为参数)内切于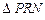 ,求
,求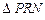 的面积的最小值.
的面积的最小值.
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
,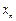 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
(本小题满分13分)
已知函数 ,
, .
.
(Ⅰ)求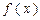 的极值;
的极值;
(Ⅱ)若 在
在 上恒成立,求
上恒成立,求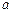 的取值范围.
的取值范围.
(本小题满分12分)
在如图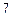 所示的几何体中,
所示的几何体中,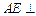 平面
平面 ,
,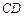 ∥
∥ ,
, 是
是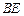 的中点,
的中点,
 ,
, ,
,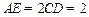 .
.
(Ⅰ)证明 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
图7