在平面直角坐标系中，已知矩形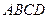
的长为２，宽为１，
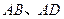边分别在ｘ轴、ｙ轴的正半轴上，
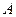点与坐标原点重合（如图4所示），将矩形折叠，使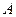点落在线段
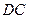上.
（Ⅰ）若折痕所在直线的斜率为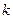
，试写出折痕所在直线的方程；
（Ⅱ）设折痕线段为EF，记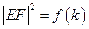
，求
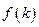的解析式.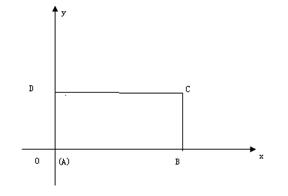
有三张形状、大小、质地完全一致的卡片，在每张卡片上分别写上0，1，2，现从中任意抽取一张，将其上的数字记作x，然后放回，再抽取一张，将其上的数字记作y，令
．
（1）求X所取各值的概率；
（2）求随机变量X的均值与方差．
在500个人身上试验某种血清预防感冒的作用，把一年中的记录与另外500个未用血清的人作比较，结果如下表所示：
| 未感冒 |
感冒 |
总计 |
|
| 试验过 |
252 |
248 |
500 |
| 未用过 |
224 |
276 |
500 |
| 总计 |
476 |
524 |
1000 |
试画出列联表的条形图，并通过图形判断这种血清能否起到预防感冒的作用？并进行独立性检验．
如图，是一个正态曲线，试根据该图象写出其正态分布密度曲线的解析式，并求出正态总体随机变量的均值和方差．
甲、乙两地都位于长江下游，根据一百多年的气象记录，知道甲、乙两地一年中雨天占的比例分别为20%和18%，两地同时下雨的比例为12%，问：
（1）乙地为雨天时甲地也为雨天的概率是多少？
（2）甲地为雨天时乙地也为雨天的概率是多少？
在平面直角坐标系内，点
的横、纵坐标都在{0，1，2，3}内取值．
（1）不同的点P共有多少个？
（2）在上述点中，不在坐标轴上的点有多少个？