阅读下面的文字,解答问题:
大家都知道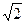 是无理数,而且
是无理数,而且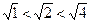 ,即
,即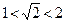 ,无理数是无限不循环小数,因此
,无理数是无限不循环小数,因此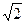 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用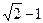 来表示
来表示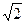 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为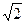 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:①∵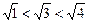 ,即
,即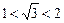 ,
,
∴ 的整数部分为1,小数部分为
的整数部分为1,小数部分为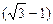 .
.
②∵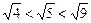 ,即
,即 ,
,
∴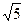 的整数部分为2,小数部分为
的整数部分为2,小数部分为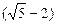 .
.
请解答: 的整
的整 数部分为 ,小数部分为 。
数部分为 ,小数部分为 。如果
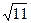 的小数部分为a,
的小数部分为a,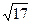 的整数部分为b
的整数部分为b ,求
,求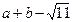 的值;(要求写出解题过程)
的值;(要求写出解题过程)
"中国结"是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正面印有"中国结"图案的不透明卡片 , , ,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中含有 卡片的概率.
先化简,再求值: ,其中 .
在平面直角坐标系中,函数 为常数)的图象与 轴交于点 .
(1)求点 的坐标.
(2)当此函数图象经过点 时,求此函数的表达式,并写出函数值 随 的增大而增大时 的取值范围.
(3)当 时,若函数 为常数)的图象的最低点到直线 的距离为2,求 的值.
(4)设 , 三个顶点的坐标分别为 、 、 .当函数 为常数)的图象与 的直角边有交点时,交点记为点 .过点 作 轴的垂线,与此函数图象的另一个交点为 与 不重合),过点 作 轴的垂线,与此函数图象的另一个交点为 .若 ,直接写出 的值.

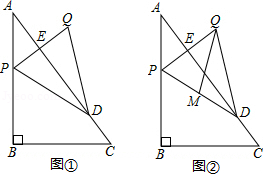
如图①,在 中, , , .点 从点 出发,沿折线 以每秒5个单位长度的速度向点 运动,同时点 从点 出发,沿 以每秒2个单位长度的速度向点 运动,点 到达点 时,点 、 同时停止运动.当点 不与点 、 重合时,作点 关于直线 的对称点 ,连结 交 于点 ,连结 、 .设点 的运动时间为 秒.
(1)当点 与点 重合时,求 的值.
(2)用含 的代数式表示线段 的长.
(3)当 为锐角三角形时,求 的取值范围.
(4)如图②,取 的中点 ,连结 .当直线 与 的一条直角边平行时,直接写出 的值.
【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .