(满分12分)
已知函数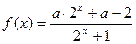 是定义在R上的奇函数.
是定义在R上的奇函数.
(1)求 的值;
的值;
(2)判断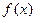 在R上的单调性并用定义证明;
在R上的单调性并用定义证明;
(3)若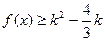 对
对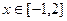 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
某校兴趣小组进行了一项“娱乐与年龄关系”的调查,对 15~65岁的人群随机抽取1000人的样本,进行了一次“是否是电影明星追星族”调查,得到如下各年龄段样本人数频率分布直方图和“追星族”统计表: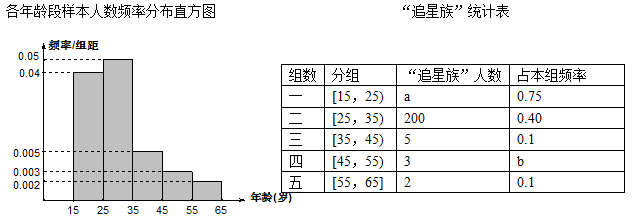
(1)求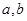 的值.
的值.
(2)设从45岁到65岁的人群中,随机抽取2人,用样本数据估计总体, 表示其中“追星族”的人数,求
表示其中“追星族”的人数,求 分布列、期望和方差.
分布列、期望和方差.
已知函数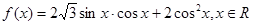 .
.
(1)求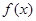 的最小正周期;
的最小正周期;
(2)已知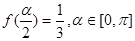 ,求
,求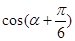 的值.
的值.
已知三棱锥P—ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB。
(1)求证明:MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,求MN的长。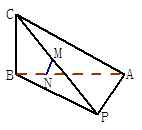
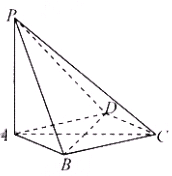
如图,在四棱锥 中,
中,
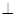 平面
平面 ,底面
,底面 是菱形,
是菱形, .
.
(1)求证: 平面
平面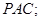
(2)若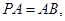 求
求 与
与 所成角的余弦值;
所成角的余弦值;
如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
求证:(1)CD⊥PD;(2)EF⊥平面PCD.