.(本小题满分12分)
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件时,该服装厂获得的利润最大,最大利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价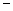 成本)
成本)
如图,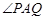 是直角,圆
是直角,圆 与射线
与射线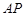 相切于点
相切于点 ,与射线
,与射线 相交于两点
相交于两点 .求证:
.求证: 平分
平分 .
.
已知函数 ,其中
,其中 ,
, 为自然对数的底数
为自然对数的底数
(1)若函数 的图像在
的图像在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值.
的值.
(2)关于 的不等式
的不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(3)讨论 极值点的个数.
极值点的个数.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率 ,左顶点为
,左顶点为 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 于点
于点 ,交
,交 轴于点
轴于点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知 为
为 的中点,是否存在定点
的中点,是否存在定点 ,对于任意的
,对于任意的 都有
都有 ,若存在,求出点
,若存在,求出点 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若过 点作直线
点作直线 的平行线交椭圆
的平行线交椭圆 于点
于点 ,求
,求 的最小值.
的最小值.
已知各项均为正数的数列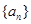 的首项
的首项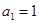 ,
, 是数列
是数列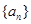 的前n项和,且满足:
的前n项和,且满足: .
.
(1)若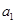 ,
, ,
, 成等比数列,求实数
成等比数列,求实数 的值;
的值;
(2)若 ,求
,求 .
.
如图, 是南北方向的一条公路,
是南北方向的一条公路, 是北偏东
是北偏东 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线 .为方便游客光,拟过曲线
.为方便游客光,拟过曲线 上的某点分别修建与公路
上的某点分别修建与公路 ,
, 垂直的两条道路
垂直的两条道路 ,且
,且 的造价分别为
的造价分别为 万元/百米,
万元/百米, 万元/百米,建立如图所示的直角坐标系
万元/百米,建立如图所示的直角坐标系 ,则曲线符合函数
,则曲线符合函数 模型,设
模型,设 ,修建两条道路
,修建两条道路 的总造价为
的总造价为 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.
(1)求 解析式;
解析式;
(2)当 为多少时,总造价
为多少时,总造价 最低?并求出最低造价.
最低?并求出最低造价.