如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2,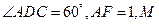 是线段EF的中点.
是线段EF的中点.
(1)求证: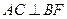 ;(2)设二面角A—FD—B的大小为
;(2)设二面角A—FD—B的大小为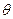 ,求
,求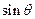 的值;
的值;
(3)设点P为一动点,若点P从M出发,沿棱按照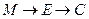 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.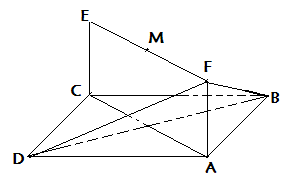
已知等差数列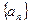 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列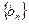 的首项为b,公比为a,其中a、b都是大于1的正整数,且
的首项为b,公比为a,其中a、b都是大于1的正整数,且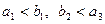 。
。
①求a的值;
②对于任意的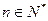 ,总存在
,总存在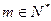 ,使得
,使得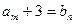 成立,求b;
成立,求b;
③令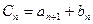 ,问数列
,问数列 中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。
中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。
设数列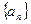 满足
满足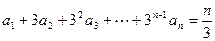
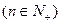
①求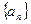 的通项公式;②设
的通项公式;②设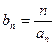 ,求数列
,求数列 的前n项和
的前n项和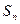 。
。
若函数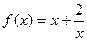 的定义域恰是能使关于x的不等式
的定义域恰是能使关于x的不等式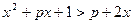 对于实数
对于实数 恒成立的充要条件,求
恒成立的充要条件,求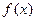 的定义域及值域。
的定义域及值域。
投资生产A产品时,每生产100吨需要资金200万元,需场地200m2,可获利润300万元,投资生产B产品时,每生产100吨需资金300万元,需场地100m2,可获利润200万元,某单位有可使用资金1400万元,场地900 m2,问作怎样的组合可获利最多?最多利润是多少?
| 资金(万元) |
场地(m2) |
利润(万元) |
|
| A产品(每百吨) |
200 |
200 |
300 |
| B产品(每百吨) |
300 |
100 |
200 |
在△ABC中,a、b、c成等比数列,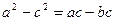
①求A的大小;②求sinB+sinC的取值。