已知函数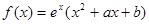 的图象在
的图象在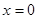 处的切线方程为
处的切线方程为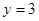 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求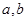 的值;
的值;
(2)当 时,证明
时,证明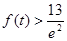 ;
;
(3)对于定义域为D的函数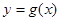 若存在区间
若存在区间 时,使得
时,使得 时,
时,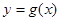 的值域是
的值域是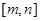 。则称
。则称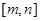 是该函数
是该函数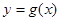 的“保值区间”。设
的“保值区间”。设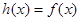 +
+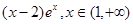 ,问函数
,问函数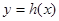 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
(本小题满分16分)
在任何两边都不相等的锐角三角形ABC中,已知角A、B、C的对边分别为a、b、c
且
(1)求角B的取值范围;
(2)求函数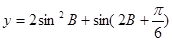 的值域;(3)求证:
的值域;(3)求证: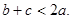
(本题满分15分)
如图所示,某学校的教学楼前有一块矩形空地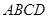 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为 米与
米与 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形 )的面积为8平方米
)的面积为8平方米
(1)试用 表示草坪的面积
表示草坪的面积 ,并指出
,并指出 的取值范围
的取值范围
(2)如何设计人行道的宽度 、
、 ,才能使草坪的面积最大?并求出草坪的最大面积。
,才能使草坪的面积最大?并求出草坪的最大面积。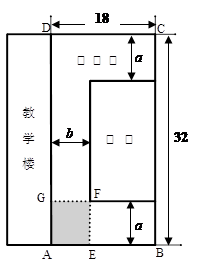
(本题满分15分)
已知二次函数 的二次项系数为
的二次项系数为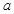 ,且不等式
,且不等式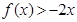 的解集为
的解集为 .
.
(1)若方程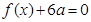 有两个相等的实数根, 求
有两个相等的实数根, 求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求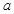 的取值范围.
的取值范围.
(本题满分14分)
等比数列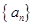 中,
中,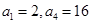 ,
,
(1)求数列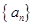 的通项公式;
的通项公式;
(2)若 分别是等差数列
分别是等差数列 的第3项和第5项,求数列
的第3项和第5项,求数列 的通项公式及前n项和
的通项公式及前n项和 .
.
(本题满分14分)
已知△ 中,
中,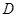 在边
在边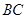 上,且
上,且 o,
o, o.
o.
(1)求 的长;
的长;
(2)求△ 的面积.
的面积.