某省两相近重要城市之间人员交流频繁，为了缓解交通压力，特修一条专用铁路，用一列火车作为交通车，已知该车每次拖4节车厢，一日能来回16次， 如果每次拖7节车厢，则每日能来回10次．
（1）若每日来回的次数是车头每次拖挂车厢节数的一次函数，求此一次函数解析式；
（2）在（1）的条件下，每节车厢能载乘客110人．问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
在△ABC中，角A，B，C的对边分别为a，b，c，且满足（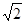
a－c）
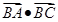＝c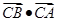 
（1）求角B的大小；
（2）若|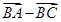
|＝
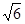，求△ABC面积的最大值．
已知数列{an}的首项a1＝1，且满足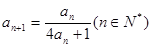
．
（1）设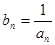
，求证：数列{bn}是等差数列，并求数列{an}的通项公式；
（2）设cn＝bn·2n，求数列{cn}的前n项和Sn．
已知函数f（x）=cosx•sin（x+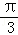
）﹣
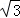cos2x+
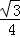，x∈R．
（1）求f（x）的最小正周期；
（2）求f（x）在闭区间[﹣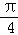
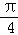，]上的最大值和最小值．
数列{an}通项公式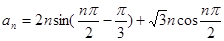
,前n项和为Sn，则S2015＝
设函数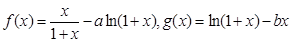
（1）若函数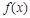
在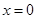
处有极值，求函数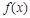的最大值；
（2）是否存在实数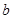
，使得关于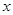
的不等式
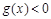在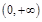
上恒成立？若存在，求出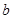的取值范围；若不存在，说明理由；
（3）证明：不等式