在中学生综合素质评价的测评中,分“优、良、不及格”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:

(Ⅰ)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为良的概率;
(Ⅱ)由表中统计数据填写下边 列联表,并判断是否有
列联表,并判断是否有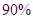 的把握认为“测评结果优秀与性别有关”.
的把握认为“测评结果优秀与性别有关”.
| |
男生 |
女生 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
参考数据与公式:
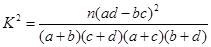 ,其中
,其中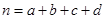 .
.
临界值表:
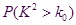 |
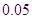 |
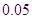 |
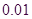 |
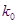 |
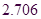 |
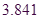 |
 |
直线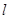 过点
过点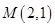 ,且与椭圆
,且与椭圆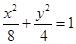 交于
交于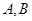 两点,
两点,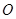 是坐标原点.
是坐标原点.
(Ⅰ)若点 是弦
是弦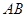 的中点,求直线
的中点,求直线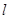 的方程;
的方程;
(Ⅱ)若直线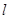 过椭圆的左焦点,求数量积
过椭圆的左焦点,求数量积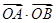 的值.
的值.
如图,已知抛物线 :
: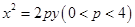 ,其上一点
,其上一点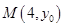 到其焦点
到其焦点 的距离为
的距离为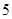 ,过焦点
,过焦点 的直线
的直线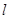 与抛物线
与抛物线 交于
交于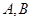 左、右两点.
左、右两点.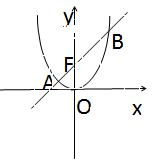
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)若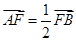 ,求直线
,求直线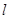 的方程.
的方程.
已知圆 的半径为
的半径为 ,圆心
,圆心 在直线
在直线 上.
上.
(Ⅰ)若圆 被直线
被直线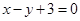 截得的弦长为
截得的弦长为 ,求圆
,求圆 的标准方程;
的标准方程;
(Ⅱ)设点 ,若圆
,若圆 上总存在两个点到点
上总存在两个点到点 的距离为
的距离为 ,求圆心
,求圆心 的横坐标
的横坐标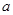 的取值范围.
的取值范围.
已知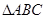 的三个顶点的坐标为
的三个顶点的坐标为 .
.
(Ⅰ)求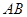 边上的高所在直线的方程;
边上的高所在直线的方程;
(Ⅱ)若直线 与
与 平行,且在
平行,且在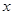 轴上的截距比在
轴上的截距比在 轴上的截距大
轴上的截距大 ,求直线
,求直线 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
在边长为4的正方形ABCD的边上有一点P沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积y值为6,则路程x的值为多少?并指出此时点P的在正方形的什么位置上?