(本小题满分12分)
从集合 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.
(1) 记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为 ,求
,求 的分布列和数学期望E
的分布列和数学期望E .
.
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,
BD交AC于点E,F是PC中点,G为EC中点.
(1)求证:FG//平面PBD;
(2)当二面角B—PC—D的大小为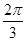 时,求FG与平面PCD所成角的正切值.
时,求FG与平面PCD所成角的正切值.
已知向量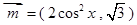 ,
,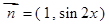 ,函数
,函数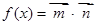
(1)求函数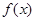 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)在
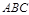 中,
中, 分别是角
分别是角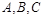 的对边,且
的对边,且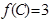 ,
, ,
, ,且
,且 ,求
,求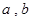 的值.
的值.
已知棱长为l的正方体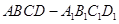 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、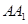 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且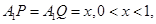 设面
设面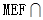 面MPQ=
面MPQ=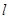 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )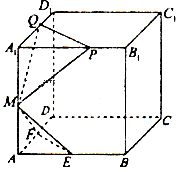
A.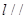 面ABCD
面ABCD
B.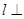 AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,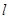 不是定直线
不是定直线
已知函数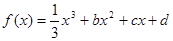 ,设曲线
,设曲线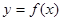 在与x轴交点处的切线为
在与x轴交点处的切线为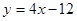 ,
,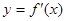 为
为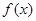 的导函数,满足
的导函数,满足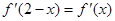 .
.
(1)求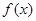 ;
;
(2)设 ,m>0,求函数
,m>0,求函数 在[0,m]上的最大值;
在[0,m]上的最大值;
(3)设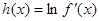 ,若对于一切
,若对于一切 ,不等式
,不等式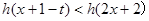 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
已知各项均为整数的数列 满足
满足 ,
, ,前6项依次成等差数列, 从第5项起依次成等比数列.
,前6项依次成等差数列, 从第5项起依次成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求出所有的正整数m ,使得 .
.