(本小题满分14分)
已知a∈R,函数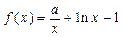 ,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在
,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在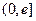 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数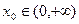 ,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
70 |
90 |
120 |
| y/μm |
6 |
10 |
10 |
13 |
16 |
17 |
19 |
23 |
25 |
29 |
46 |
用散点图及相关系数两种方法判断x与y的相关性.
下表是对某市8所中学学生是否吸烟进行调查所得的结果:
| 吸烟学生 |
不吸烟学生 |
|
| 父母中至少有一人吸烟 |
816 |
3 203 |
| 父母均不吸烟 |
188 |
1 168 |
(1)在父母至少有一人吸烟的学生中,估计吸烟学生所占的百分比是多少?
(2)在父母均不吸烟的学生中,估计吸烟学生所占的百分比是多少?
(3)学生的吸烟习惯和父母是否吸烟有关吗?请简要说明理由.
(4)有多大的把握认为学生的吸烟习惯和父母是否吸烟有关?
从发生汽车碰撞事故的司机中抽取2 000名司机.根据他们的血液中是否含有酒精以及他们是否对事故负有责任.将数据整理如下:
| 有责任 |
无责任 |
合计 |
|
| 有酒精 |
650 |
150 |
800 |
| 无酒精 |
700 |
500 |
1 200 |
| 合计 |
1 350 |
650 |
2 000 |
那么,司机对事故负有责任与血液中含有酒精是否有关系?
有甲、乙两个工厂生产同一种产品,产品分为一等品和二等品.为了考察这两个工厂的产品质量的水平是否一致,从甲、乙两个工厂中分别随机地抽出产品109件,191件,其中甲工厂一等品58件,二等品51件,乙工厂一等品70件,二等品121件.
(1)根据以上数据,建立2×2列联表;
(2)试分析甲、乙两个工厂的产品质量有无显著差别(可靠性不低于99%).
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下所示:
| 又发作过心脏病 |
未发作过心脏病 |
合计 |
|
| 心脏搭桥手术 |
39 |
157 |
196 |
| 血管清障手术 |
29 |
167 |
196 |
| 合计 |
68 |
324 |
392 |
比较这两种手术对病人又发作心脏病的影响有没有差别.