(本小题满分12分)
设函数
(I)用五点法画出它在一个周期内的闭区间上的图象;
(II)求函数f(x)的最小正周期及函数f(x)的最大值
(III)求函数f(x)的单调增区间。
如图,在四棱 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。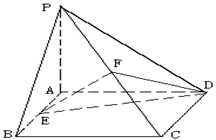
⑴求证:CD⊥PD;
⑵求证:EF∥平面PAD;
⑶若直线EF⊥平面PCD,求平面PCD与平面ABCD所成二面角的大小
设函数 ,其中向量
,其中向量
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)在ΔABC中,角A、B、C所对的边分别为a、b、c,若 ,且
,且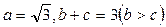 ,求
,求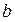 与
与 的值。
的值。
已知等差数列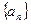 中,
中, ,前10项和
,前10项和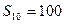 .
.
(1)求数列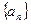 的通项公式;
的通项公式;
(2)设 ,证明
,证明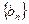 为等比数列,并求
为等比数列,并求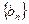 的前四项之和。
的前四项之和。
(3)设 ,求
,求 的前五项之和。
的前五项之和。
(1)已知 ,
, ,求
,求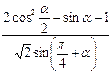 的值;
的值;
(2)已知 ,且
,且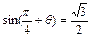 ,求
,求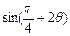 的值
的值
设M是由满足下列条件的函数 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 的导数
的导数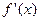 满足
满足 ”
”
(I)证明:函数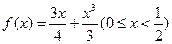 是集合M中的元素;
是集合M中的元素;
(II)证明:函数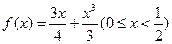 具有下面的性质:对于任意
具有下面的性质:对于任意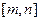
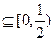 ,都存在
,都存在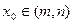 ,使得等式
,使得等式 成立。
成立。