（ 7分）
已知数列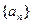
中，
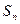是它的前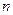
项和，并且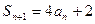
，
。
（1）设
，求证
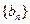是等比数列
（2）设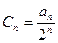
，求证
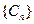是等差数列
（3）求数列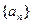的通项公式及前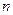项和公式
已知命题
“方程
表示焦点在
轴上的椭圆”,
命题
“方程
表示双曲线”．
（1）若
是真命题,求实数
的取值范围；
（2）若
是真命题,求实数
的取值范围；
（3）若“
”是真命题,求实数的取值范围．
已知双曲线C的方程为：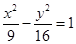 
（1）求双曲线C的离心率；
（2）求与双曲线C有公共的渐近线，且经过点A（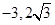
）的双曲线的方程。
定义在（0，＋∞）上的函数f（x），对于任意的m，n∈（0，＋∞），都有f（mn）＝f（m）＋f（n）成立，当x＞1时，f（x）＜0．
（1）求证：1是函数f（x）的零点；
（2）求证：f（x）是（0，＋∞）上的减函数；
（3）当f （2）＝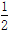 
时，解不等式f （ax＋4）＞1．
当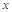
满足
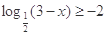时，求函数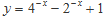
的最值及相应的
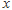的值．
已知二次函数
满足
．
（1）求的解析式；
（2）若在
上有最小值
，最大值
，求a的取值集合．