(本小题满分14分)
在锐角△ABC中,已知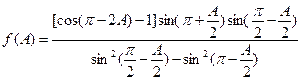 .
.
(1)求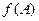 的最大值;
的最大值;
(2)当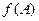 取得最大值时,
取得最大值时, ,如果
,如果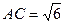 ,求
,求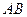 边和
边和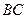 边的长.
边的长.
某外商到一开放区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,有两种处理方案: ①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为v千米/小时、2v千米/小时、10v千米/小时,每千米的运费分别为a元、b元、c元.且b<a<c,又这批海鲜在运输过程中的损耗为m元/小时,若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等.试确定使用哪种运输工具总费用最省.(题中字母均为正的已知量)
小宁中午放学回家自己煮面条吃,有下面几道工序: (1)洗锅盛水2分钟;(2)洗菜6分钟;(3)准备面条及佐料2分钟;(4)用锅把水烧开10分钟;(5)煮面条和菜共3分钟.以上各道工序除(4)之外,一次只能进行一道工序,小宁要将面条煮好,最少用分钟.
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,问当a、b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?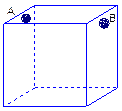
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律 每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=
每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=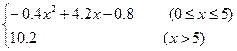 .假定该产品销售平衡,那么根据上述统计规律.
.假定该产品销售平衡,那么根据上述统计规律.
(1)要使工厂有盈利,产品x应控制在什么范围?
(2)工厂生产多少台产品时赢利最大?并求此时每台产品的售价为多少?