(本题满分13分)
已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在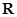 上有三个零点.
上有三个零点.
(1)求 的值;
的值;
(2)若1是其中一个零点,求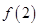 的取值范围;
的取值范围;
(3)若 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
(本小题满分12分)已知椭圆C: ,若椭圆C上的一动点到右焦点的最短距离为
,若椭圆C上的一动点到右焦点的最短距离为 ,且右焦点到直线
,且右焦点到直线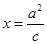 的距离等于短半轴的长,已知P
的距离等于短半轴的长,已知P ,过P的直线与椭圆交于M、N两点
,过P的直线与椭圆交于M、N两点
(Ⅰ)求椭圆C的方程
(Ⅱ)求 的取值范围
的取值范围
(本小题满分12分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,△APB面积的最大值为2 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线AP的倾斜角为 ,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
(本小题满分12分)已知函数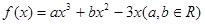 ,在点
,在点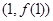 处的切线方程为
处的切线方程为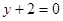 .
.
(Ⅰ)求函数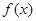 的解析式;
的解析式;
(Ⅱ)若对于区间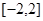 上任意两个自变量的值
上任意两个自变量的值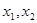 ,都有
,都有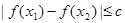 ,求实数
,求实数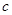 的最小值;
的最小值;
已知命题p: 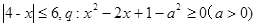 ,若非p是q的充分不必要条件,求a的取值范围。
,若非p是q的充分不必要条件,求a的取值范围。
直线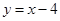 与抛物线
与抛物线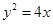 交于A、B两点,F为抛物线的焦点,求△ABF的面积。
交于A、B两点,F为抛物线的焦点,求△ABF的面积。