(本小题满分16分)已知函数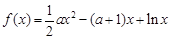 ,
, 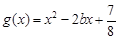 .
.
(Ⅰ)当 时,求曲线
时,求曲线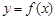 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当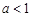 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当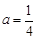 时,函数
时,函数 在
在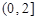 上的最大值为
上的最大值为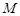 ,若存在
,若存在 ,使得
,使得
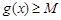 成立,求实数b的取值范围.
成立,求实数b的取值范围.
(本小题满分14分)
已知向量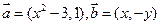 ,(其中实数
,(其中实数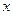 和
和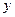 不同时为零),当
不同时为零),当 时,有
时,有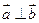 ,当
,当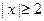 时,
时,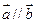 .
.
(1)求函数式 ;
;
(2)求函数 的单调递减区间;
的单调递减区间;
(3)若对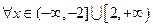 ,都有
,都有 ,求实数
,求实数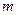 的取值范围.
的取值范围.
(本小题满分14分)
已知点C(1,0),点A、B是⊙O: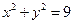 上任意两个不同的点,且满足
上任意两个不同的点,且满足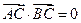 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线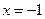 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.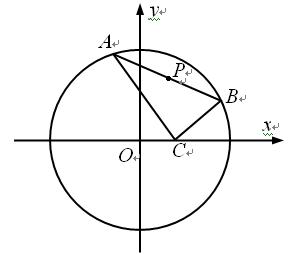
(本小题满分14分)
如图,四边形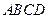 为矩形,且
为矩形,且 ,
,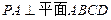 ,
, 为
为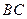 上的动点.
上的动点.
(1) 当 为
为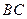 的中点时,求证:
的中点时,求证: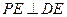 ;
;
(2) 设 ,在线段
,在线段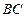 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角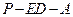 的平面角大小为
的平面角大小为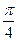 . 试确定点E的位置.
. 试确定点E的位置.
(本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的分布列与期望。
(本小题满分 分)
分)
设三角形 的内角
的内角 的对边分别为
的对边分别为
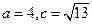 ,
,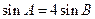 .
.
(1)求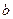 边的长;
边的长;
(2)求角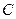 的大小;
的大小;
(3)求三角形 的面积
的面积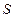 。
。