(本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的分布列与期望。
已知圆 .
.
(1)若直线 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的方程;
的方程;
(2)若圆 的半径为4,圆心
的半径为4,圆心 在直线
在直线 :
: 上,且与圆
上,且与圆 内切,求圆
内切,求圆 的方程.
的方程.
已知 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部; :
: 都有
都有 .
.
(1)若 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若 为假命题,求
为假命题,求 的取值范围;
的取值范围;
(3)若“ 且
且 ”为假命题,且“
”为假命题,且“ 或
或 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
如图,设椭圆 :
:
 的离心率
的离心率 ,顶点
,顶点 的距离为
的距离为 ,
, 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点.
两点.
(ⅰ)试判断点 到直线
到直线 的距离是否为定值.若是请求出这个定值,若不是请说明理由;
的距离是否为定值.若是请求出这个定值,若不是请说明理由;
(ⅱ)求 的最小值.
的最小值.
已知函数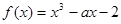 在
在 处达到极值,
处达到极值,
(1)求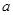 的值;
的值;
(2)若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,在四棱锥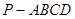 中,底面为直角梯形,
中,底面为直角梯形, ,
, ,
, 底面
底面 ,且
,且 ,
,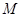 、
、 分别为
分别为 、
、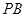 的中点.
的中点.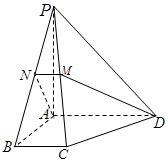
(1)求证: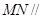 平面
平面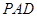 ;
;
(2)求证: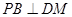 .
.