已知函数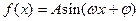
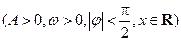 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数 的解析式;
的解析式;
(2)当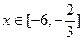 时,求函数
时,求函数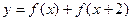 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
已知数列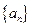 的前n项和为
的前n项和为 ,且
,且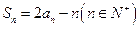 .
.
(1)求数列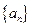 的通项;
的通项;
(2)若数列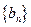 中,
中,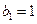 ,点P(
,点P(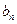 ,
,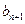 )在直线
)在直线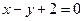 上,记
上,记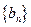 的前n项和为
的前n项和为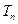 ,当
,当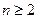 时,试比较
时,试比较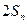 与
与 的大小.
的大小.
(13分)已知椭圆C的中心在坐标原点,离心率 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线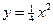 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S(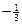 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
(12分)如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为A1D1和CC1 的中点.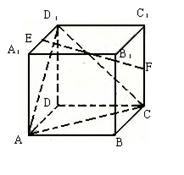
(1)求证:EF∥平面ACD1;
(2)求面EFB与底面ABCD所成的锐二面角余弦值的大小.
(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率;
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率;
(3)求该同学获得奖金 的数学期望(精确到元).
的数学期望(精确到元).
(12分)已知向量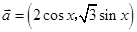 ,
,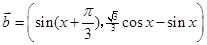 ,函数
,函数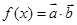 .
.
(1)求函数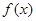 的最小正周期;
的最小正周期; (2)若
(2)若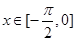 时,求
时,求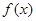 的单调递减区间;
的单调递减区间;