已知动圆C过点A(-2,0),且与圆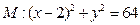 相内切。
相内切。
(1)求动圆C的圆心的轨迹方程;
(2)设直线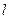 : y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线
: y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线
交于不同两点E,F,问是否存在直线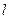 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知椭圆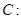
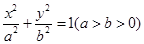 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知动直线 与椭圆
与椭圆 相交于
相交于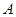 、
、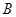 两点。
两点。
①若线段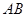 中点的横坐标为
中点的横坐标为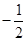 ,求斜率
,求斜率 的值;
的值;
②已知点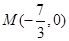 ,求证:
,求证: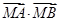 为定值
为定值
若 是函数
是函数 的两个极值点。
的两个极值点。
(Ⅰ)若 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)若 ,求
,求 的最大值。
的最大值。
如图,已知直四棱柱 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, ,
, 分别是棱
分别是棱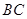 ,
, 上的动点,且
上的动点,且 ,
, ,
,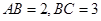 .
.
(Ⅰ)证明:无论点 怎样运动,四边形
怎样运动,四边形 都为矩形;
都为矩形;
(Ⅱ)当 时,求几何体
时,求几何体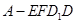 的体积。
的体积。
已知数列 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
, 。
。
(I)求数列 的通项公式;(II)设
的通项公式;(II)设 求数列
求数列 的前n项和Sn。
的前n项和Sn。
已知关于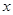 的一元二次函数
的一元二次函数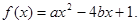
(Ⅰ)设集合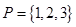 和
和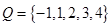 ,分别从集合
,分别从集合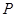 和
和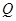 中随机取一个数作为
中随机取一个数作为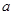 和
和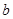 ,求函数
,求函数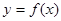 在区间[
在区间[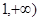 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点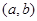 是区域
是区域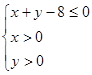 内的随机点,记
内的随机点,记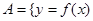 有两个零点,其中一个大于
有两个零点,其中一个大于 ,另一个小于
,另一个小于
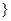 ,求事件
,求事件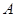 发生的概率
发生的概率