设命题 :
: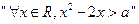 ,命题
,命题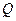 :
: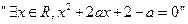 ;如果“
;如果“ 或
或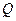 ”为真,“
”为真,“ 且
且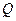 ”为假,求
”为假,求 的取值范围。
的取值范围。
已知 ,(其中
,(其中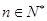 )
)
⑴求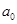 及
及 ;
;
⑵试比较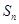 与
与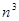 的大小,并说明理由.
的大小,并说明理由.
数列 首项
首项 ,前
,前 项和
项和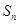 满足等式
满足等式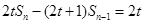 (常数
(常数 ,
,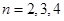 ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使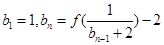 (
(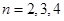 ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
在 中,已知
中,已知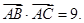
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
已知等比数列 中,
中, ,且
,且 ,公比
,公比 ,(1)求
,(1)求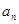 ;(2)设
;(2)设 ,求数列
,求数列 的前
的前 项和
项和
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。