由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高。然而也有部分公众对该活动的实际效果与负面影响提出了疑问。对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| |
支持 |
保留 |
不支持 |
| 20岁以下 |
800 |
450 |
200 |
| 20岁以上(含20岁) |
100 |
150 |
300 |
⑴在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持”态度的人中抽取了45个人,求n的值;
⑵在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中
任意选取2人,求至少1人20岁以下的概率;
⑶在接受调查的人中,有8人给这项活动打出了分数如下:9.4, 8.6, 9.2, 9.6, 8.7
9.3, 9.0, 8.2.把这8人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过0.6的概率。
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合;
的取值集合;
(Ⅱ)已知 中,角A,B,C的对边分别为a,b,c若
中,角A,B,C的对边分别为a,b,c若 b+c=2。求实数a的取值范围。
b+c=2。求实数a的取值范围。
已知无穷数列 的各项均为正整数,
的各项均为正整数, 为数列
为数列 的前
的前 项和.
项和.
(Ⅰ)若数列 是等差数列,且对任意正整数
是等差数列,且对任意正整数 都有
都有 成立,求数列
成立,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数 ,从集合
,从集合 中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与
中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与 一起恰好是1至
一起恰好是1至 全体正整数组成的集合.
全体正整数组成的集合.
(ⅰ)求 的值;(ⅱ)求数列
的值;(ⅱ)求数列 的通项公式.
的通项公式.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求 的取值范围.
的取值范围.
若椭圆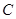 的方程为
的方程为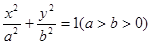 ,
, 、
、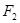 是它的左、右焦点,椭圆
是它的左、右焦点,椭圆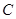 过点
过点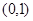 ,且离心率为
,且离心率为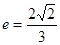 .
.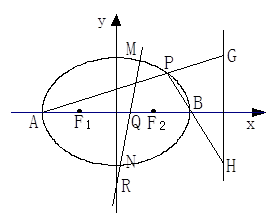
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左右顶点为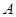 、
、 ,直线
,直线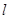 的方程为
的方程为 ,
,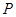 是椭圆上任一点,直线
是椭圆上任一点,直线 、
、 分别交直线
分别交直线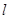 于
于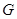 、
、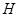 两点,求
两点,求 的值;
的值;
(Ⅲ)过点 任意作直线
任意作直线 (与
(与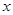 轴不垂直)与椭圆
轴不垂直)与椭圆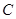 交于
交于 、
、 两点,与
两点,与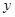 轴交于
轴交于 点
点 ,
, .证明:
.证明: 为定值.
为定值.
如图①,一条宽为1km的两平行河岸有三个工厂 、
、 、
、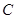 ,工厂
,工厂 与
与 、
、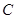 的直线距离都是2km,
的直线距离都是2km, 与河岸垂直,
与河岸垂直,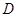 为垂足.现要在河岸
为垂足.现要在河岸 上修建一个供电站,并计划铺设地下电缆和水下电缆,从供电站向三个工厂供电.已知铺设地下电缆、水下电缆的费用分别为2万元/km、4万元/km.
上修建一个供电站,并计划铺设地下电缆和水下电缆,从供电站向三个工厂供电.已知铺设地下电缆、水下电缆的费用分别为2万元/km、4万元/km.
(Ⅰ)已知工厂 与
与 之间原来铺设有旧电缆(原线路不变),经改造后仍可使用,旧电缆的改造费用是0.5万元/km.现决定将供电站建在点
之间原来铺设有旧电缆(原线路不变),经改造后仍可使用,旧电缆的改造费用是0.5万元/km.现决定将供电站建在点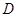 处,并通过改造旧电缆修建供电线路,试求该方案总施工费用的最小值;
处,并通过改造旧电缆修建供电线路,试求该方案总施工费用的最小值;
(Ⅱ)如图②,已知供电站建在河岸 的点
的点 处,且决定铺设电缆的线路为
处,且决定铺设电缆的线路为 、
、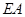 、
、 ,若
,若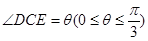 ,试用
,试用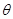 表示出总施工费用
表示出总施工费用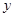 (万元)的解析式,并求总施工费用
(万元)的解析式,并求总施工费用 的最小值.
的最小值.