在平面直角坐标系xOy中,曲线C1的参数方程为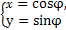 (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为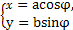 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=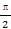 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值.
(2)设当α=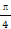 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=-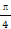 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
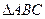 的内角
的内角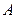 、
、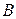 、
、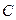 的对边分别为
的对边分别为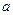 、
、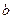 、
、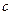 。
。
己知 .
.
(Ⅰ)求
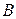 ;
;
(Ⅱ)若
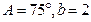 ,求.
,求. 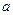 、
、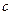
设等比数列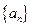 的前n项和为
的前n项和为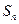 ,已知
,已知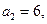
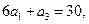 求
求 和
和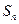 .
.
(本小题满分15分)
已知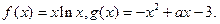
(Ⅰ)求函数 上的最小值;
上的最小值;
(Ⅱ)若对一切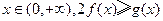 恒成立,求实数
恒成立,求实数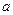 的取值范围;
的取值范围;
(Ⅲ)证明:对一切 ,都有
,都有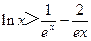 成立.
成立.
(本小题满分15分)
已知椭圆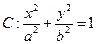
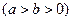 的离心率为
的离心率为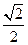 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线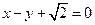 相切.
相切.
(Ⅰ)求椭圆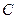 的方程;
的方程;
(Ⅱ)若过点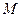 (2,0)的直线与椭圆
(2,0)的直线与椭圆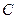 相交于两点
相交于两点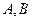 ,
,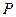 为椭圆上一点,且满足
为椭圆上一点,且满足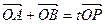 (
(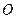 为坐标原点),当
为坐标原点),当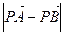 <
< 时,求实数
时,求实数 的取值范围.
的取值范围.
(本小题满分14分)
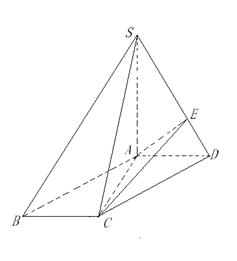
如图,在四棱锥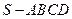 中,底面
中,底面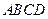 为平行四边形,
为平行四边形,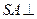 平面
平面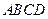 ,
,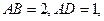
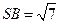
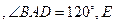 在棱
在棱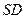 上
上 .
.
(Ⅰ)当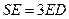 时,求证
时,求证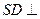 平面
平面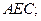
(Ⅱ)当二面角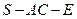 的大小为
的大小为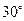 时,求直线
时,求直线 与平面
与平面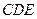 所成角的正弦值.
所成角的正弦值.