已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范围为[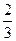 ,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
(本小题满分7分)选修4—5:不等式选讲
已知函数 .
.
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)设 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分7分)《选修4-4:坐标系与参数方程》
已知曲线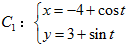 (
(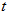 为参数),
为参数),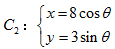 (
(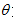 为参数).
为参数).
(Ⅰ)化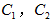 的方程为普通方程;
的方程为普通方程;
(Ⅱ)若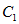 上的点对应的参数为
上的点对应的参数为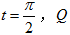 为
为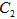 上的动点,求
上的动点,求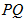 中点
中点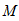 到直线
到直线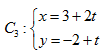 (
(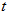 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系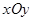 中,把矩阵
中,把矩阵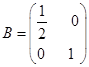 确定的压缩变换
确定的压缩变换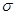 与矩阵
与矩阵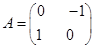 确定的旋转变换
确定的旋转变换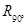 进行复合,得到复合变换
进行复合,得到复合变换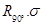 .
.
(Ⅰ)求复合变换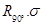 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆C:x2+ y2 =1在复合变换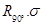 的作用下所得曲线
的作用下所得曲线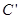 的方程.
的方程.
(本小题满分14分)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
如图,已知椭圆 :
: 的离心率为
的离心率为 ,以椭圆
,以椭圆 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与椭圆
与椭圆 交于点
交于点 与点
与点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的最小值,并求此时圆
的最小值,并求此时圆 的方程;
的方程;
(3)设点 是椭圆
是椭圆 上异于
上异于 ,
, 的任意一点,且直线
的任意一点,且直线 分别与
分别与 轴交于点
轴交于点 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.