已知椭圆C: ,在曲线C上是否存在不同两点A、B关于直线
,在曲线C上是否存在不同两点A、B关于直线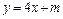 (m为常数)对称?若存在,求出
(m为常数)对称?若存在,求出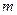 满足的条件;若不存在,说明理由。
满足的条件;若不存在,说明理由。
在如图所示的空间几何体中,平面 平面
平面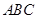 ,
, 是边长为2的等边三角形,
是边长为2的等边三角形,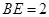 ,
,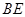 和平面
和平面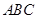 所成的角为60°,且点
所成的角为60°,且点 在平面
在平面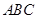 上的射影落在
上的射影落在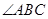 的平分线上.
的平分线上.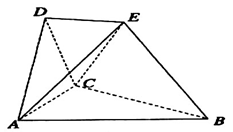
(1)求证: //平面
//平面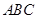 ;
;
(2)求二面角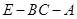 的余弦值.
的余弦值.
如图,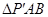 是边长为
是边长为 的等边三角形,
的等边三角形, 现将
现将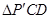 沿边
沿边 折起至
折起至 得四棱锥
得四棱锥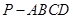 , 且
, 且

(1)证明:
 平面
平面 ;
;
(2)求四棱锥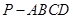 的体积.
的体积.
已知 展开式中各项的系数之和比各项的二项式系数之和大
展开式中各项的系数之和比各项的二项式系数之和大 .
.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
已知一个袋内有4只不同的红球,6只不同的白球。
(1)从中任取4只球,红球的只数不比白球少的取法有多少种?
(2)若取一只红球记2分,取一只红球记2分,取一只白球记1分,从中任取5只球,使总分不小于7分的取法有多少种?
(3)在(2)条件下,当总分为8时,将抽出的球排成一排,仅有两个红球相邻的排法种数是多少?
解下列方程: