设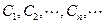 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在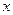 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线 相切,对每一个正整数
相切,对每一个正整数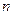 ,圆
,圆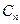 都与圆
都与圆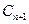 相互外切,以
相互外切,以 表示
表示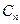 的半径,已知
的半径,已知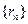 为递增数列.
为递增数列.
(Ⅰ)证明: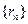 为等比数列;
为等比数列;
(Ⅱ)设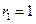 ,求数列
,求数列 的前
的前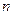 项和.
项和.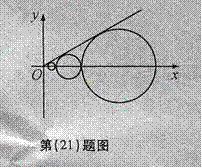
已知函数f(x)=(ax2﹣2x+a)e﹣x
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)设 ,若x>l时总有g(x)<h(x),求实数c范围.
,若x>l时总有g(x)<h(x),求实数c范围.
如图,椭圆C: +
+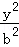 =1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=
=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|= |BF|.
|BF|.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ.求直线l的方程及椭圆C的方程.
已知函数f(x)=x2+2x+alnx(a∈R).
(1)当时a=﹣4时,求f(x)的最小值;
(2)若函数f(x)在区间(0,1)上为单调函数,求实数a的取值范围.
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有 2Sn=2 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1= .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an•cn,(n为正整数),求数列{dn}的前n项和Tn.
已知数列{an}的前n项和Sn,a1=﹣ ,Sn+
,Sn+ (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn= ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣ .
.