如图，椭圆C：
+
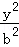=1（a＞b＞0）的右焦点为F，右顶点、上顶点分别为点A、B，且|AB|=
|BF|．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）若斜率为2的直线l过点（0，2），且l交椭圆C于P、Q两点，OP⊥OQ．求直线l的方程及椭圆C的方程．
在平面直角坐标系上，设不等式组
（
）
所表示的平面区域为
，记内的整点（即横坐标和纵坐标均为整数的点）的个数为
.
（Ⅰ）求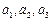
并猜想
的表达式再用数学归纳法加以证明；
（Ⅱ）设数列
的前
项和为
，数列
的前项和
,是否存在自然数m？使得对一切，
恒成立。若存在，求出m的值，若不存在，请说明理由。
设圆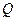
过点P(0,2), 且在
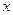轴上截得的弦RG的长为4.
(１)求圆心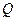的轨迹E的方程；
(２)过点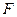
(０，１)，作轨迹
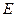的两条互相垂直的弦
、
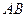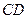，设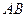、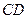的中点分别为
、
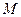，试判断直线
是否过定点？并说明理由．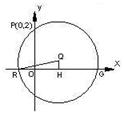
如图，四棱锥S—ABCD的底面是边长为1的正方形，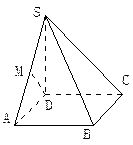
SD垂直于底面ABCD，SB=
.
（I）求证BC
SC；
（II）求面ASD与面BSC所成二面角的大小；
（III）设棱SA的中点为M，求异面直线DM与SB所成角的大小.
已知函数
图像上一点
处的切线方程为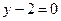
，其中
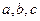为常数.
（Ⅰ）函数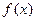
是否存在单调减区间？若存在，则求出单调减区间（用
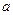表示）；
（Ⅱ）若
不是函数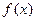的极值点，求证：函数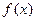的图像关于点
对称.
已知命题
：方程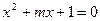
有两个不等的负实根；
：方程
无实根．若“或”为真，“且”为假，求实数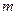
的取值范围．