在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点, =2
=2 =2.
=2.
(1)求证: ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求三棱锥 的体积
的体积 .
.
如图,四棱锥S-ABCD中,SD 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.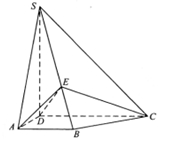
(Ⅰ)求证:无论E点取在何处恒有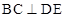 ;
;
(Ⅱ)设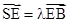 ,当平面EDC
,当平面EDC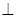 平面SBC时,求
平面SBC时,求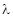 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角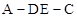 的大小.
的大小.
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是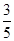 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是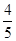 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用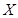 表示张同学答对题的个数,求
表示张同学答对题的个数,求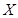 的分布列和数学期望.
的分布列和数学期望.
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 .
.
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
已知在等比数列 中,
中,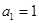 ,且
,且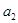 是
是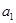 和
和 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,求
,求 的前
的前 项和
项和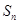 .
.
已知函数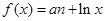 ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定 的单调区间:
的单调区间:
(II)若f(x)在区间 (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明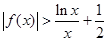 .
.