(文科做)(本小题满分16分)
已知椭圆 过点
过点 ,离心率为
,离心率为 ,圆
,圆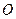 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆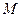 的方程为
的方程为 .过圆
.过圆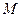 上任一点
上任一点 作圆
作圆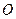 的切线
的切线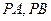 ,切点为
,切点为 .
.
(1)求椭圆的方程;
(2)若直线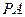 与圆
与圆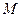 的另一交点为
的另一交点为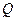 ,当弦
,当弦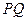 最大时,求直线
最大时,求直线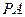 的直线方程;
的直线方程;
(3)求 的最值.
的最值.
.在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
.任意投掷两枚骰子,计算:(1)出现点数相同的概率;(2)出现点数和为奇数的概率、
14、如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现 有均匀的豆子散落在正方形中,问豆子落在中间带形区域的概率是多少?
有均匀的豆子散落在正方形中,问豆子落在中间带形区域的概率是多少?
如右图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D.
(Ⅰ)求∠ADF的度数;
(Ⅱ)若AB=AC,求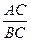 的值.
的值.
已知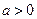 ,设命题
,设命题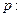 函数
函数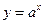 在R上单调递减,
在R上单调递减,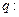 不等式
不等式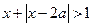 的解集为R,若
的解集为R,若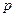 和
和 中有且只有一个命题为真命题,求
中有且只有一个命题为真命题,求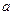 的取值范围.
的取值范围.