(本小题满分10)选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.
(1)证明: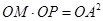 ;
;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点。过B点的切
线交直线ON于K。证明:∠OKM = 90°.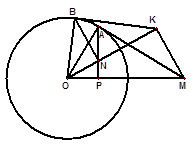
点A、B分别是以双曲线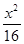
 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,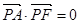
(1)求椭圆C的的方程;
(2)求点P的坐标;
(3)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值。
2013年全国第十二届全运会由沈阳承办。城建部门计划在浑南新区建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数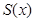 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
点P是圆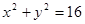 上的一个动点,过点P作PD垂直于
上的一个动点,过点P作PD垂直于 轴,垂足为D,Q为线段PD的中点。
轴,垂足为D,Q为线段PD的中点。
(1)求点Q的轨迹方程。
(2)已知点M(1,1)为上述所求方程的图形内一点,过点M作弦AB,若点M恰为弦AB的中点,求直线AB的方程。
已知等差数列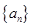 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
(1)求通项公式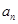
(2)设 ,求数列
,求数列 的前
的前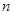 项和
项和 。
。
(1)若 ,求
,求 的最大值。
的最大值。
(2) 为何值时,直线
为何值时,直线 和曲线
和曲线 有两个公共点。
有两个公共点。