（本小题满分14分）等比数列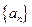
中，
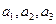分别是下表第一、二、三行中的某一个数，且
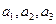中的任何两个数不在下表的同一列.
| |
第一列 |
第二列 |
第三列 |
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
（Ⅰ）
求数列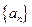的通项公式；
（Ⅱ）若数列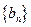
满足 
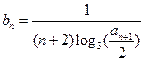，记数列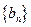的前n项和为
，证明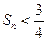
已知函数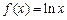
（Ⅰ）求函数
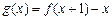的最大值；（Ⅱ）当
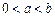时，求证: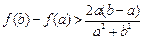
.
用一枚质地均匀的硬币，甲、乙两人做抛掷硬币游戏，甲抛掷4次，记正面朝上的次为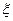
；乙抛掷3次，记正面朝上的次为
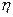.（Ⅰ）分别求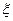和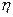的期望；（Ⅱ）规定：若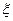>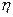，则甲获胜；否则，乙获胜.求甲获胜的概率.
已知函数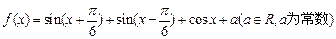
.(Ⅰ)求函数
的最小正周期；(Ⅱ)若函数在[-
，]上的最大值与最小值之和为
，求实数
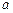的值.
袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个，从中每次任取1个．有放回地抽取3次，求：
(1)3个全是红球的概率． (2)3个颜色全相同的概率．
(3)3个颜色不全相同的概率． (4)3个颜色全不相同的概率．
由经验得知，在某商场付款处排队等候付款的人数及概率如下表：
| 排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
| 概率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
(1)至多有2人排队的概率是多少? (2)至少有2人排队的概率是多少?