(本小题满分14分)给定函数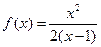
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,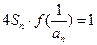 求证:
求证: ;
;
(3)设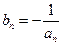 ,
,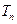 为数列
为数列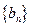 的前
的前 项和,求证:
项和,求证: 。
。
(本小题12分)已知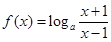 (
(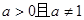 ).
).
(1)判断函数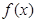 的奇偶性,并证明;
的奇偶性,并证明;
(2)若 ,用单调性定义证明函数
,用单调性定义证明函数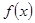 在区间
在区间 上单调递减;
上单调递减;
(3)是否存在实数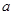 ,使得
,使得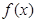 的定义域为
的定义域为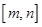 时,值域为
时,值域为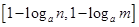 ,若存在,求出实数
,若存在,求出实数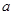 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
(本小题12分)某公司生产一种产品每年需投入固定成本为0.5万元,此外每生产100件这种产品还需要增加投入0.25万元.经预测知,当售出这种产品 百件时,若
百件时,若 ,则销售所得的收入为
,则销售所得的收入为 万元:若
万元:若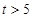 ,则销售收入为
,则销售收入为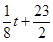 万元.
万元.
(1)若该公司的这种产品的年产量为 百件
百件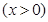 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润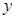 表示为当年生产量
表示为当年生产量 的函数;
的函数;
(2)当年产量为多少时,当年公司所获利润最大?
(本小题12分)已知函数
(1)若函数 的值域为
的值域为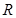 ,求实数
,求实数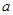 的取值范围;
的取值范围;
(2)当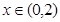 时,函数
时,函数 恒有意义,求实数
恒有意义,求实数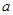 的取值范围。
的取值范围。
(本小题满分12分)
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AB∥CD,BA⊥AD,且CD=2AB.
(1)若AB=AD=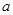 ,直线PB与CD所成角为
,直线PB与CD所成角为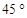 ,
,
①求四棱锥P-ABCD的体积;
②求二面角P-CD-B的大小;
(2)若E为线段PC上一点,试确定E点的位置,使得平面EBD垂直于平面ABCD,并说明理由.
(本小题满分12分)
如图,正方体 中, E是
中, E是 的中点.
的中点. 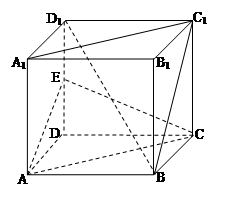
(1)求证: ∥平面AEC;
∥平面AEC;
(2)求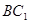 与平面
与平面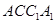 所成的角.
所成的角.