已知椭圆C: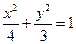 ,过点
,过点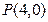 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线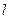 交椭圆
交椭圆 于
于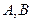 两点,设点
两点,设点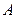 关于
关于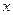 轴的对称点为
轴的对称点为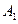 ,
,
(1)求证:直线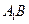 过
过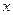 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(2)求: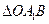 面积的取值范围。
面积的取值范围。
“坐标法”是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究图形的几何性质的方法,它是解析几何中是基本的研究方法. 请用坐标法证明下面问题:
已知圆O的方程是 ,点
,点 ,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是
,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是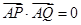 .
.
在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
,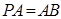 ,点
,点 是
是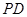 的中点,作
的中点,作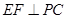 交
交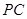 于
于 .
.
(Ⅰ)求证: ∥平面
∥平面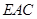 ;
;
(Ⅱ)求证: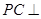 平面
平面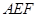 ;
;
(Ⅲ)求二面角 的大小.
的大小.
已知等差数列{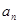 },公差
},公差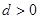 ,
,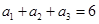 ,且
,且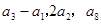 成等比数列.
成等比数列.
(I)求{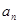 }的通项公式;
}的通项公式;
(II)设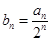 ,求证:
,求证: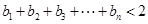 .
.
在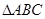 中,内角
中,内角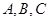 对边分别为
对边分别为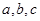 ,且
,且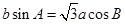 .
.
(Ⅰ)求角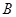 的大小;
的大小;
(Ⅱ)若 ,求
,求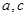 的值.
的值.
(本小题满分14分)
已知函数 (
( ).
).
(1)若 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 的最小值是1,求实数
的最小值是1,求实数 的值.
的值.