(本小题满分12分) 已知定义在正实数集上的函数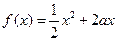 ,
, ,其中
,其中 .设两曲线
.设两曲线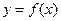 ,
, 有公共点,且在该点处的切线相同
有公共点,且在该点处的切线相同
(I)用 表示
表示 ,并求
,并求 的最大值;
的最大值;
(II)求证: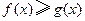 (
( )
)
(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数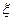 的分别列与期望E
的分别列与期望E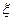 .
.
(本小题满分10分) 已知 的面积为
的面积为 ,且满足
,且满足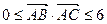 ,设
,设 和
和 的夹角为
的夹角为
(I)求 的取值范围;
的取值范围;
(II)求函数 的最大值与最小值
的最大值与最小值
(本小题满分12分)已知数列{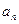 }满足
}满足 =
=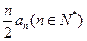 ,
, 是{
是{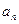 }的前
}的前 项的和,
项的和, .(1)求
.(1)求 ;(2)证明:
;(2)证明: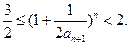
已知菱形ABCD与矩形BDEF所在平面互相垂直,且BD=2BF,若M为EF的中点。
⑴求证:BM∥平面AEC;
⑵求证:平面AEC⊥平面AFC;
⑶若AF与平面BDEF成600角,求二面角A-BM-D的余弦值。