若存在实常数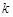 和
和 ,使得函数
,使得函数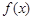 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线
 为
为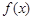 和
和 的“隔离直线”.已知
的“隔离直线”.已知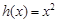 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求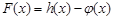 的极值;
的极值;
(2) 函数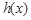 和
和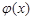 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知:在△ABC中,cosA = .(1)求cos2 – sin(B+C)的值;(2)如果△ABC的面积为4,AB =" 2" ,求BC的长.
在 中,三边
中,三边 、
、 、
、 对角分别为
对角分别为 、
、 、
、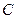 ,且
,且
(1)求角 的余弦值;(2)若
的余弦值;(2)若 ,且
,且 ,求
,求 和
和 的值.
的值.
已知函数 ,
, .(1)求函数
.(1)求函数 在
在 内的单调递增区间;
内的单调递增区间;
(2)若函数 在
在 处取到最大值,求
处取到最大值,求 的值;
的值;
(3)若 (
( ),求证:方程
),求证:方程 在
在 内没有实数解.(参考数据:
内没有实数解.(参考数据: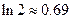 ,
,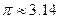 )
)
已知角 为
为 的三个内角,其对边分别为
的三个内角,其对边分别为 ,若
,若 ,
, ,
, ,且
,且 .(1)若
.(1)若 的面积
的面积 ,求
,求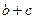 的值.(2)求
的值.(2)求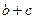 的取值范围.
的取值范围.
设函数f(x)=cos(2x+ )+sin
)+sin x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为
x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.