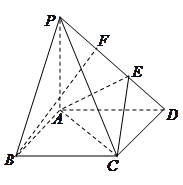(本小题满分14分)
已知函数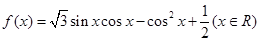 .
.
(1)求函数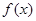 的最小正周期;
的最小正周期;
(2)求函数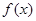 在区间
在区间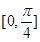 上的函数
上的函数 值的取值范围.
值的取值范围.
(12分)已知函数 过
过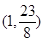 点,且关于
点,且关于 成中心对称.
成中心对称.
(1)求函数 的解析式;
的解析式;
(2)数列 满足
满足 .求证:
.求证:
 .
.
.(12分)已知椭圆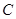 的中心在原点,
的中心在原点,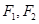 分别为它的左、右焦点,直线
分别为它的左、右焦点,直线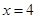 为它的一条准线,又知椭圆
为它的一条准线,又知椭圆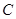 上存在点
上存在点 ,使得
,使得 .
.
(1)求椭圆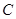 的方程;
的方程;
(2)若 是椭圆
是椭圆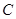 上不与椭圆顶点重合的任意两点,点
上不与椭圆顶点重合的任意两点,点 关于
关于 轴的对称点是
轴的对称点是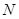 ,直线
,直线 分别交
分别交 轴于点
轴于点 ,点
,点 ,探究
,探究 是否为定值,若为定值,求出该定值,若不为定值,请说明理由.
是否为定值,若为定值,求出该定值,若不为定值,请说明理由.
12分)已知 是数列
是数列 的前
的前 项和,且对任意
项和,且对任意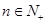 ,有
,有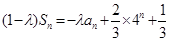 .记
.记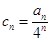 .其中
.其中 为实数,且
为实数,且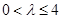 .
.
(1)当 时,求数列
时,求数列 的通项;
的通项;
(2)当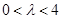 时,若
时,若 对任意
对任意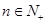 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(13分)四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,
, ,
,  为
为 上两点,且
上两点,且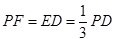 .
.
(1)求证: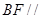 面
面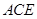 ;
;
(2)求异面直线PC与AE所成的角
(3)求二面角 的正切值.
的正切值.