如图，已知抛物线
经过点
，抛物线的顶点为
，过
作射线
．过顶点平行于
轴的直线交射线
于点
，
在轴正半轴上，连结
．求该抛物线的解析式；
动点
从点出发，以每秒1个长度单位的速度沿射线运动，设点运动的时间为
．问当
为何值时，四边形
分别为平行四边形？直角梯形？等腰梯形？若
，动点和动点
分别从点和点同时出发，分别以每秒1个长度单位和2个长度单位的速度沿
和
运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为
，连接
，当为何值时，四边形
的面积最小？并求出最小值及此时的长．
已知：关于x的一元二次方程mx 2-（3m+2）x+2m+2=0（m>0）．
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x 1，x 2（其中x 1< x 2）．若y是关于x的函数，且y=x 2-2x 1，求这个函数的解析式．
已知一个二次函数y=ax 2+bx+c的图象如图所示，请求出这个二次函数的解析式。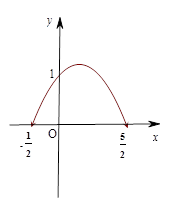 
如图，不用量角器，在方格纸中画出△ABC绕点B顺时针方向旋转90°后得到的△A １BC １．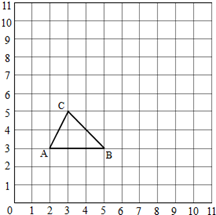 
解方程： 
点A、B、C在同一直线上，在直线AC的同侧作△ABE和△BCF，连接AF，CE．取AF、CE的中点M、N，连接BM，BN，MN．
（1）若△ABE和△FBC是等腰直角三角形，且∠ABE=∠FBC=90°（图1），则△MBN是______三角形；
（2）在△ABE和△BCF中，若BA=BE，BC=BF，且∠ABE=∠FBC=α，（图2），则△MBN是______三角形，且∠MBN=______；
（3）若将（2）中的△ABE绕点B旋转一定角度，（图3），其他条件不变，那么（2）中的结论是否成立？若成立，给出你的证明；若不成立，写出正确的结论并给出证明．