按右图的流程，输入一个数据x，根据y与x的函数关系式就 输出一个数据y，这样可以将一组数据变换成另一组新的数据，要使任意一组都在20到100（含20和100）之间的数据，变换成一组新数据后能满足下列两个要求：
（ⅰ）、新数据都在60到100（含60和100）之间。
（ⅱ）、新数据之间的大小关系与原数据之间的大小关系一致，即原数据大的对应的新数据也较大。问：若y与x的关系式是 y=x+p(100-x),请说明：当p=
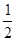时，这种变换满足上述两个要求。若按关系式：y=a(x-h)2+k(a﹥0)将数据进行变换，请写出一个满足上述要求的这种关系式。（不要求对关系式符合题意作说明，但要求写出关系式得出的主要过程）
如图，点P是菱形ABCD的对角线BD上的一点，连接CP并延长 ，交AD于E，交BA的延长线于F。
（1）求证：∠DCP=∠DAP．
（2）若AB=2，DP:PB=1:2，且PA⊥BF，求对角线BD的长。
关于
的一元二次方程2＋2＋
＋1=O的实数解是1和2；
（1）求的取值范围；
（2）如果1＋2－12＜－1，且为整数，求的值。
已知如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC，过点C作⊙O的切线，交OD的延长线于点E，连接BE：
（1）求证：BE是⊙O的切线；
（2）连接AD并延长交BE于点F，若OB=9，Sin∠ABC=
，求BF的长。
某班数学科代表小红对本班上学期期末考试成绩（成绩取整数，满分100分）作了统计分析，绘制成如下 频数，频率统计表和频率分布直方图。请你根据图表中提供的信息解答下列问题，
（1）频数频率表中的a=____b=____；
（2）补全频数分布直方图；
（3）小红在班上任选一名同学，该同学数学成绩不低于80分的概率是多少？
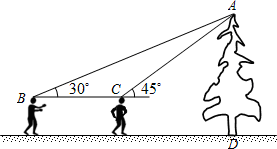
某校初三学生去社会实践，在风景区看到一棵汉白杨树，好高哟，数学老师说请小明和小华同学用数学知识测量，全体同学计算这棵树多高，下面是这两位同学的对话。
小明：我站在此处看到树顶仰角45°;
小华：我站在此处看到树顶仰角30°
小明、小华身高都是1．6米，两人相距20米，请你来根据两位同学的对话，结合图形，算出这棵汉白杨的高（参考数据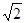
≈1．414
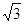≈1．732，结果保留三个有效字）。