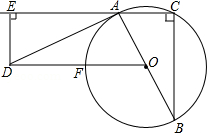
已知如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC，过点-优题课

小甘到文具超市去买文具．请你根据如图中的对话信息，求中性笔和笔记本的单价分别是多少元？

二次函数 $y = a x^{2} + bx + 2$ 的图象交 $x$ 轴于点 $(- 1, 0)$ ， $B (4, 0)$ 两点，交 $y$ 轴于点 $C$ ．动点 $M$ 从点 $A$ 出发，以每秒2个单位长度的速度沿 $AB$ 方向运动，过点 $M$ 作 $MN ⊥ x$ 轴交直线 $BC$ 于点 $N$ ，交抛物线于点 $D$ ，连接 $AC$ ，设运动的时间为 $t$ 秒．

（1）求二次函数 $y = a x^{2} + bx + 2$ 的表达式；

（2）连接 $BD$ ，当 $t = \frac{3}{2}$ 时，求 $ΔDNB$ 的面积；

（3）在直线 $MN$ 上存在一点 $P$ ，当 $ΔPBC$ 是以 $∠ BPC$ 为直角的等腰直角三角形时，求此时点 $D$ 的坐标；

（4）当 $t = \frac{5}{4}$ 时，在直线 $MN$ 上存在一点 $Q$ ，使得 $∠ AQC + ∠ OAC = 90 °$ ，求点 $Q$ 的坐标．

通过对下面数学模型的研究学习，解决问题．

【模型呈现】

如图，在 $Rt Δ ABC$ ， $∠ ACB = 90 °$ ，将斜边 $AB$ 绕点 $A$ 顺时针旋转 $90 °$ 得到 $AD$ ，过点 $D$ 作 $DE ⊥ AC$ 于点 $E$ ，可以推理得到 $ΔABC ≅ ΔDAE$ ，进而得到 $AC = DE$ ， $BC = AE$ ．

我们把这个数学模型称为“ $K$ 型”．

推理过程如下：

【模型应用】

如图，在 $Rt Δ ABC$ 内接于 $⊙ O$ ， $∠ ACB = 90 °$ ， $BC = 2$ ，将斜边 $AB$ 绕点 $A$ 顺时针旋转一定的角度得到 $AD$ ，过点 $D$ 作 $DE ⊥ AC$ 于点 $E$ ， $∠ DAE = ∠ ABC$ ， $DE = 1$ ，连接 $DO$ 交 $⊙ O$ 于点 $F$ ．

（1）求证： $AD$ 是 $⊙ O$ 的切线；

（2）连接 $FC$ 交 $AB$ 于点 $G$ ，连接 $FB$ ．求证： $F G^{2} = GO \cdot GB$ ．

如图，在 $ΔABC$ 中， $AB = AC = 6 cm$ ， $BC = 8 cm$ ，点 $D$ 为 $BC$ 的中点， $BE = DE$ ，将 $∠ BDE$ 绕点 $D$ 顺时针旋转 $α$ 度 $(0 ⩽ α ⩽ 83 °)$ ，角的两边分别交直线 $AB$ 于 $M$ 、 $N$ 两点，设 $B$ 、 $M$ 两点间的距离为 $xcm$ ， $M$ ， $N$ 两点间的距离为 $ycm$ ．

小涛根据学习函数的经验，对函数 $y$ 随自变量 $x$ 的变化而变化的规律进行了探究．

下面是小涛的探究过程，请补充完整．

（1）列表：下表的已知数据是 $B$ ， $M$ 两点间的距离 $x$ 进行取点、画图、测量，分别得到了 $y$ 与 $x$ 的几组对应值：

$x / cm$	0	0.30	0.50	1.00	1.50	2.00	2.50	$\frac{8}{3}$	3.00	3.50	3.68	3.81	3.90	3.93	4.10
$y / cm$		2.88	2.81	2.69	2.67	2.80	3.15		3.85	5.24	6.01	6.71	7.27	7.44	8.87

请你通过计算，补全表格；

（2）描点、连线，在平面直角坐标系 $xOy$ 中，描出表格中各组数值所对应的点 $(x, y)$ ，并画出函数 $y$ 关于 $x$ 的图象．

（3）探究性质：随着自变量 $x$ 的不断增大，函数 $y$ 的变化趋势：　　．

（4）解决问题：当 $MN = 2 BM$ 时， $BM$ 的长度大约是　　 $cm$ ．（保留两位小数）．

某数学课题研究小组针对兰州市住房窗户“如何设计遮阳蓬”这一课题进行了探究，过程如下：

问题提出：

如图1是某住户窗户上方安装的遮阳蓬，要求设计的遮阳蓬能最大限度地遮住夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内．

方案设计：

如图2，该数学课题研究小组通过调查研究设计了垂直于墙面 $AC$ 的遮阳蓬 $CD$ ．

数据收集：

通过查阅相关资料和实际测量：兰州市一年中，夏至日这一天的正午时刻太阳光线 $DA$ 与遮阳蓬 $CD$ 的夹角 $∠ ADC$ 最大 $(∠ ADC = 77.44 °)$ ；冬至日这一天的正午时刻，太阳光线 $DB$ 与遮阳蓬 $CD$ 的夹角 $∠ BDC$ 最小 $(∠ BDC = 30.56 °)$ ．窗户的高度 $AB = 2 m$ ．

问题解决：

根据上述方案及数据，求遮阳蓬 $CD$ 的长．

（结果精确到 $0.1 m$ ，参考数据： $\sin 30.56 ° \approx 0.51$ ， $\cos 30.56 ° \approx 0.86$ ， $\tan 30.56 ° \approx 0.59$ ， $\sin 77.44 ° \approx 0.98$ ， $\cos 77.44 ° \approx 0.22$ ， $\tan 77.44 ° \approx 4.49)$