(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:(1) FD∥平面ABC; (2) AF⊥平面EDB.

(1) 已知曲线C :
: (t为参数), C
(t为参数), C :
: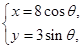 (
( 为参数)。化C
为参数)。化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)求两个圆ρ=4cosθ 0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
已知函数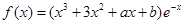
(1)如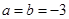 ,求
,求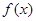 的单调区间;
的单调区间;
(2)若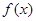 在
在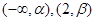 单调增加,在
单调增加,在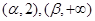 单调减少,
单调减少,
证明: o.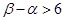
已知函数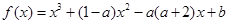
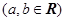 .
.
(1)若函数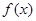 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是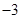 ,求
,求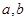 的值;
的值;
(2)若函数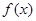 在区间
在区间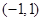 上不单调,求
上不单调,求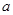 的取值范围.
的取值范围.
已知二次函数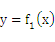 的图像的顶点为原点,且过
的图像的顶点为原点,且过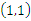 ,反比例函数
,反比例函数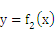 的图像与直线y="x的两个交点间距离为8,已知"
的图像与直线y="x的两个交点间距离为8,已知" 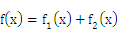
(1)求函数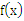 的表达式;
的表达式;
(2)试证明:当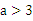 时,关于x的方程
时,关于x的方程 有三个实数解。
有三个实数解。
对于函数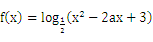 ,解答下列问题:
,解答下列问题:
(1)若 定义域为R,求实数a的取值范围;
定义域为R,求实数a的取值范围;
(2)若函数 在
在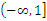 内为增函数,求实数a的取值范围.
内为增函数,求实数a的取值范围.